ほのにっき 🍄
Back to blog
•
4 min read

統計力学で解き明かす！気体入り円筒は本当に「回しにくい」のか？

#統計力学 #物理 #理論 #院試
Table of Contents

導入

フィギュアスケートの選手がスピンをするとき、腕を広げると回転が遅くなり、腕を体に引き寄せると速くなります。これは「慣性モーメント」が変化するためです。慣性モーメントは、物体の「回しにくさ」を表す量で、質量が回転軸から遠くに分布するほど大きくなります。

では、こんな疑問を考えてみましょう。大学院入試の物理問題でも題材にされるような、少し思考力を要する問題です。

同じ総質量を持つ「中身が空っぽの円筒」と「気体が入った円筒」、回しやすいのはどっち？

直感的には、中身が詰まっている方が回しにくそうに感じるかもしれません。しかし、気体は自由に動き回れる粒子のかたまりです。この「気体の自由さ」は、回しやすさにどう影響するのでしょうか？

この記事では、統計力学の考え方を用いて、この疑問を解き明かしていきます。

1. 舞台設定：回転する円筒の中の気体たち

今回の舞台は、角速度 ω\omega でz軸周りに回転する円筒形の容器です。この中には、温度 TT で熱平衡状態にある理想気体が閉じ込められています。容器も気体も、一緒になって回転しているのがポイントです。

気体粒子一つ一つは、デタラメな方向に飛び回る「熱運動」をしています。しかし、容器が回転しているため、全粒子は遠心力を感じて外側（円筒の壁側）に押しやられます。

確率分布

このときの粒子1個の状態は、以下の「確率密度関数」p(r,p)p(\mathbf{r}, \mathbf{p}) で記述されます。これは回転する系におけるカノニカル分布です。

p(r,p)=1h3LZ~1exp⁡(−H1(r,p)−ωM1(r,p)kT)p(\mathbf{r}, \mathbf{p}) = \frac{1}{h^3L\tilde{Z}_1} \exp\left(-\frac{H_1(\mathbf{r}, \mathbf{p}) - \omega M_1(\mathbf{r}, \mathbf{p})}{kT}\right)

重要なのは指数部分の H1−ωM1H_1 - \omega M_1 です。これは回転する座標系で考えたときの、粒子1個が持つ「有効なエネルギー」と解釈できます。このエネルギーが低い状態ほど、粒子は存在しやすくなります。

この式を詳しく見ると、粒子は回転軸から遠いほどエネルギー的に不安定になる「遠心力ポテンシャル」を感じていることがわかります。一方で、粒子は温度 TT に応じた熱エネルギーで運動もしています。この「外側へ向かう力」と「自由に飛び回ろうとする熱運動」のせめぎあいが、今回の問題を解く鍵となります。

2. 気体の「回しにくさ」＝慣性モーメントを計算する旅

それでは、この気体の慣性モーメント IgasI_{\text{gas}} を計算していきましょう。慣性モーメントは、物体の各部分の質量 mim_i と、その部分の回転軸からの距離 rir_i を使って、I=∑imiri2I = \sum_i m_i r_i^2 と表される「回しにくさ」の指標でした。

気体のように連続的に質量が分布している場合は、ある場所 r\mathbf{r} に粒子が存在する確率と、軸からの距離の2乗 (x2+y2)(x^2+y^2) を掛け合わせて、容器全体で積分（合計）することで求めます。粒子の存在確率は、先ほどの確率密度関数 p(r,p)p(\mathbf{r}, \mathbf{p}) から計算できます。

この統計力学的な計算を実行すると、気体の慣性モーメント IgasI_{\text{gas}} が、気体の総質量 NmNm、温度 TT、容器の半径 RR と角速度 ω\omega などにどう依存するかが明らかになります。

3. 結論：空洞円筒 vs 気体入り円筒、勝者はどっち？

いよいよ結論です。計算した気体の慣性モーメント IgasI_{\text{gas}} を、「空洞円筒」の慣性モーメントと比較してみましょう。

比較対象：「空洞円筒」とは何か？

まず、比較の基準となる「空洞円筒」の正体をはっきりさせておきましょう。

ここで言う空洞円筒とは、気体と同じ総質量 NmNm を持つ物質が、半径 RR の円筒の側面に均一に張り付いている状態を指します。その慣性モーメント IcylinderI_{\text{cylinder}} は、全ての質量が回転軸から最も遠い距離 RR にあるため、次のように計算できます。

Icylinder=(Nm)R2I_{\text{cylinder}} = (Nm) R^2

この状態は、物理的に次のように見なすことができます。 「もし気体粒子が熱運動を一切やめて、遠心力によって全粒子が壁にびっしりと張り付いたとしたら…という、気体の極限状態」 これが、私たちの比較対象である「空洞円筒」の物理的なイメージです。

2.5 気体の慣性モーメントの計算（統計力学アプローチ）

それでは、前節で定義された気体の状態から、その慣性モーメント IgasI_{\text{gas}} を具体的に計算してみましょう。慣性モーメントは、気体を構成する全粒子 NN の、回転軸からの距離の2乗の平均値 ⟨x2+y2⟩\langle x^2+y^2 \rangle を使って次のように定義されます。

Igas=N⋅m⟨x2+y2⟩I_{\text{gas}} = N \cdot m \langle x^2 + y^2 \rangle

この統計平均 ⟨… ⟩\langle \dots \rangle は、粒子1個の確率密度関数（カノニカル分布）を使って計算します。

⟨x2+y2⟩=∫(x2+y2)exp⁡(−β(H1−ωM1))drdp∫exp⁡(−β(H1−ωM1))drdp\langle x^2 + y^2 \rangle = \frac{ \int (x^2+y^2) \exp\left(-\beta (H_1 - \omega M_1)\right) d\mathbf{r}d\mathbf{p} }{ \int \exp\left(-\beta (H_1 - \omega M_1)\right) d\mathbf{r}d\mathbf{p} }

ここで β=1/(kT)\beta = 1/(kT) です。この積分を計算するために、指数の中身 H1−ωM1H_1 - \omega M_1 を整理します。

H1−ωM1=12m(px2+py2+pz2)−ω(xpy−ypx)H_1 - \omega M_1 = \frac{1}{2m}(p_x^2+p_y^2+p_z^2) - \omega(xp_y - yp_x)

この式は、運動量 p\mathbf{p} と位置 r\mathbf{r} が混ざっていて積分しにくいので、運動量の項を平方完成します。

H1−ωM1=12m[(px+mωy)2+(py−mωx)2+pz2]−12mω2(x2+y2)H_1 - \omega M_1 = \frac{1}{2m}\left[ (p_x+m\omega y)^2 + (p_y-m\omega x)^2 + p_z^2 \right] - \frac{1}{2}m\omega^2(x^2+y^2)

この変形が計算の鍵です。式の前半部分は運動量のみに依存する項、後半部分は位置のみに依存する「有効ポテンシャル」 Ueff(r)=−12mω2(x2+y2)U_{\text{eff}}(r) = -\frac{1}{2}m\omega^2(x^2+y^2) となっています。

このおかげで、⟨x2+y2⟩\langle x^2 + y^2 \rangle の計算における運動量 p\mathbf{p} の積分は、分子と分母で全く同じ形になるため、互いに打ち消し合います。結果として、計算は位置座標 r\mathbf{r} だけの積分に帰着します。

⟨x2+y2⟩=∫cylinder(x2+y2)e−βUeffdr∫cylindere−βUeffdr=∫(x2+y2)eβmω22(x2+y2)dr∫eβmω22(x2+y2)dr\langle x^2 + y^2 \rangle = \frac{ \int_{\text{cylinder}} (x^2+y^2) e^{-\beta U_{\text{eff}}} d\mathbf{r} }{ \int_{\text{cylinder}} e^{-\beta U_{\text{eff}}} d\mathbf{r} } = \frac{ \int (x^2+y^2) e^{\frac{\beta m\omega^2}{2}(x^2+y^2)} d\mathbf{r} }{ \int e^{\frac{\beta m\omega^2}{2}(x^2+y^2)} d\mathbf{r} }

この積分は、円筒座標 (r,θ,z)(r, \theta, z) を使うと簡単になります。x2+y2=r2x^2+y^2 = r^2、体積素片 dr=rdrdθdzd\mathbf{r} = r dr d\theta dz となり、積分範囲は 0≤r≤R0 \le r \le R、0≤θ≤2π0 \le \theta \le 2\pi、−L/2≤z≤L/2 -L/2 \le z \le L/2 です。zz と θ\theta に依存する項はないため、これらの積分は分子分母でキャンセルされ、残るのは rr の積分だけです。

⟨r2⟩=∫0Rr2⋅eαr2⋅rdr∫0Reαr2⋅rdr=∫0Rr3eαr2dr∫0Rreαr2dr\langle r^2 \rangle = \frac{\int_0^R r^2 \cdot e^{\alpha r^2} \cdot r dr}{\int_0^R e^{\alpha r^2} \cdot r dr} = \frac{\int_0^R r^3 e^{\alpha r^2} dr}{\int_0^R r e^{\alpha r^2} dr}

ここで、計算を簡単にするため無次元のパラメータ α=mω22kT\alpha = \frac{m\omega^2}{2kT} を導入しました。

この積分は、分母の積分 I(α)=∫0Rreαr2drI(\alpha) = \int_0^R r e^{\alpha r^2} dr を計算し、その α\alpha に関する微分 I′(α)=∫0Rr3eαr2drI'(\alpha) = \int_0^R r^3 e^{\alpha r^2} dr を利用するとエレガントに解くことができます。

まず分母は、

I(α)=∫0Rreαr2dr=[12αeαr2]0R=12α(eαR2−1)I(\alpha) = \int_0^R r e^{\alpha r^2} dr = \left[ \frac{1}{2\alpha} e^{\alpha r^2} \right]_0^R = \frac{1}{2\alpha} (e^{\alpha R^2} - 1)

次に分子は、この I(α)I(\alpha) を α\alpha で微分して、

∫0Rr3eαr2dr=dI(α)dα=ddα(eαR2−12α)=R2eαR22α−eαR2−12α2\int_0^R r^3 e^{\alpha r^2} dr = \frac{dI(\alpha)}{d\alpha} = \frac{d}{d\alpha}\left( \frac{e^{\alpha R^2} - 1}{2\alpha} \right) = \frac{R^2 e^{\alpha R^2}}{2\alpha} - \frac{e^{\alpha R^2} - 1}{2\alpha^2}

したがって、これらの比を取ることで平均値が求まります。

⟨r2⟩=I′(α)I(α)=R2eαR22α−eαR2−12α2eαR2−12α=R2eαR2eαR2−1−1α\langle r^2 \rangle = \frac{I'(\alpha)}{I(\alpha)} = \frac{\frac{R^2 e^{\alpha R^2}}{2\alpha} - \frac{e^{\alpha R^2} - 1}{2\alpha^2}}{\frac{e^{\alpha R^2} - 1}{2\alpha}} = R^2 \frac{e^{\alpha R^2}}{e^{\alpha R^2}-1} - \frac{1}{\alpha}

ここで、さらに無次元のパラメータ ε=αR2=mω2R22kT\varepsilon = \alpha R^2 = \frac{m\omega^2 R^2}{2kT} を導入すると、

⟨r2⟩=R2(eεeε−1−1ε)\langle r^2 \rangle = R^2 \left( \frac{e^{\varepsilon}}{e^{\varepsilon}-1} - \frac{1}{\varepsilon} \right)

とまとめることができます。

これにより、気体全体の慣性モーメント IgasI_{\text{gas}} が導出できました。

気体入りシリンダーの慣性モーメント Igas=Nm⟨r2⟩=NmR2(eεeε−1−1ε)I_{\text{gas}} = N m \langle r^2 \rangle = N m R^2 \left( \frac{e^{\varepsilon}}{e^{\varepsilon}-1} - \frac{1}{\varepsilon} \right)

ただし、ε=mω2R22kT\varepsilon = \frac{m\omega^2 R^2}{2kT} は、回転によるエネルギーと熱エネルギーの比を表す重要な指標です。

この式は一見複雑ですが、重要なのは、ε>0\varepsilon > 0 のとき、括弧 (… )\left( \dots \right) の中が常に1より小さいということです。これは、eε>1+εe^\varepsilon > 1+\varepsilon から証明できます。

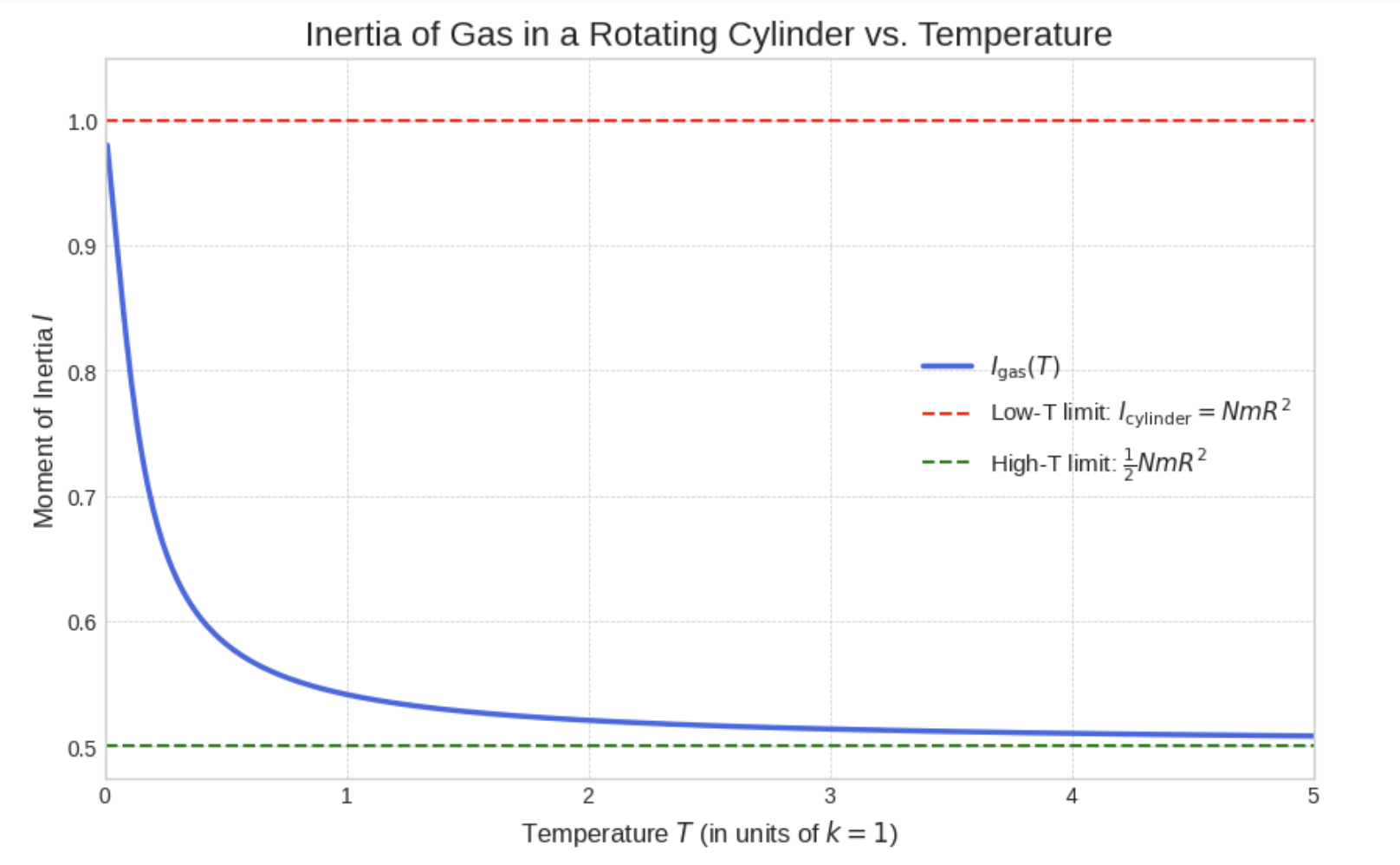
graph

このグラフからもわかる通り、高温では半減することがわかりますね。

比較と考察：熱運動が勝敗を分ける

さて、IgasI_{\text{gas}} と IcylinderI_{\text{cylinder}} はどちらが大きいでしょうか？

結論から言うと、温度が絶対零度でない限り、常に Igas<IcylinderI_{\text{gas}} < I_{\text{cylinder}} となります。

Igas<NmR2I_{\text{gas}} < NmR^2

つまり、同じ総質量であれば、気体入り円筒の方が空洞円筒よりも慣性モーメントが小さく、「回しやすい」 のです！

なぜなら、気体粒子は「壁に張り付こうとする遠心力」と「自由に飛び回ろうとする熱運動」の綱引きの中で存在しているからです。

  • 空洞円筒: 全ての質量が、回転軸から最も遠い半径 RR の位置に完全に集中しています。
  • 気体入り円筒: 粒子は遠心力で外側に追いやられるものの、熱運動によってその力に抗い、円筒の内部（中心軸に近い部分）にも必ず分布しています。

慣性モーメントは、質量と「軸からの距離の2乗」の積で決まります。気体の場合、たとえ少数でも中心近くに粒子が存在することが、全体の慣性モーメントを劇的に押し下げる効果を持っているのです。

温度による変化：極限状態を想像する

この綱引きの様子は、温度 TT を変化させることで、より鮮明に理解できます。

  • 低温極限 (T→0T \to 0): 温度をどんどん下げていくと、粒子の暴れ馬のような熱運動（エネルギー kTkT）はどんどん静かになります。すると、回転による遠心力の影響が相対的に支配的になります。その結果、粒子たちはエネルギーが最も低くなる円筒の壁際へ、壁際へと追いやられていきます。

    そして絶対零度という極限では、熱運動は完全に停止し、全ての粒子が壁に張り付いてしまいます。この状態は、私たちが先ほど定義した「空洞円筒」そのものです。

    だからこそ、低温極限において、気体の慣性モーメント IgasI_{\text{gas}} は、空洞円筒の慣性モーメント IcylinderI_{\text{cylinder}} に限りなく近づいていくのです。

  • 高温極限 (T→∞T \to \infty): 逆に温度を上げていくと、熱運動が非常に激しくなり、遠心力の影響を振り切って、粒子は円筒内をほぼ一様に飛び回るようになります。この場合、中心付近に存在する粒子の割合が大きく増えるため、慣性モーメントはさらに小さくなります。（計算上は、中身が詰まった「剛体の」円柱の慣性モーメントである Igas→12NmR2I_{\text{gas}} \to \frac{1}{2}NmR^2 に近づきます。）

まとめ、感想

今回の統計力学の旅から、以下のことが明らかになりました。

  1. 問いへの答え: 同じ総質量なら、気体入り円筒の方が空洞円筒よりも回しやすい（慣性モーメントが小さい）。
  2. その理由: 気体粒子は熱運動によって中心付近にも分布するため。質量が外側に集中している空洞円筒よりも、全体の慣性モーメントが小さくなる。
  3. 物理の面白さ: ミクロな粒子（原子・分子）の集団的な振る舞いを記述する「統計力学」を用いることで、マクロな世界の物体の性質（慣性モーメント）を見事に説明できる。

「中身が詰まっている方が重くて回しにくそう」という最初の直感は、粒子の自由な運動を考慮すると、必ずしも正しくないことが分かりました。物理学は、そんな直感を鮮やかに裏切ってくれる面白さも持っています。

ボルツマン分布はどうして指数関数になるのか？数値シミュレーションで確かめてみた
ガロア理論への招待