ほのにっき 🍄
Back to blog
•
6 min read

グロス・ピタエフスキー方程式(GP方程式)で超流動回してみた！

#偏微分方程式 #数値計算 #シミュレーション #理論 #物理 #研究
Table of Contents

超流動とGP方程式

グロス・ピタエフスキー方程式とは、超流動状態を記述する非線形偏微分方程式であり、以下のように定義される。 iℏ∂ψ∂t=[ℏ22m∇2+V(r)+g∣ψ(r)∣2]ψ(r)i\hbar \frac{\partial \psi}{\partial t} = \left[ \frac{\hbar^2}{2m}\nabla^2 +V(r) + g|\psi(r)|^2\right]\psi(r)

超流動状態

超流動状態とは液体の粘性抵抗が消失する状態です。この状態が実現すると、超流動液体が容器の壁を勝手に登ってきたり、通常の液体では通り抜けられないほど細い隙間から抜け出すなど、流動性が超上昇する現象です。超伝導状態の、電気抵抗が減少する現象と似ていますね。実はこの二つには共通の機構が眠っています。

超流動状態はボソンの巨視的な凝縮により生じます。ボソンはフェルミオンと違い同一のエネルギー状態に複数の粒子が共存できるので、最低エネルギーにボソンが全て集まり同じ状態を形成します。同一の状態で波動関数の位相が揃い、全粒子が一斉に波の振幅を強め合うことで、電子がまるで津波のような巨大な波を形成するようになります。この状態では、多少不純物があろうが波が崩れずに伝播可能なので、摩擦なしでいくらでも流動することができるようになるのです。これが超流動状態の機構です。このような凝縮のことをボース・アインシュタイン凝縮と呼びます。

超流動に転移する際には物理量が発散したり、不連続な挙動をとるなど、系が質的に激変します。水が氷になると激変するのと同様、4-ヘリウムのようなボソンも冷却すると相転移を引き起こして系の様子を全くもって変化させるのです。

グロス・ピタエフスキー方程式(GP方程式)

そんな波が”自己増幅”して相転移する様子を現象論的に記述したのが**グロス・ピタエフスキー方程式(GP方程式)**です。方程式は先ほど同様以下のようになります。

iℏ∂ψ∂t=[−ℏ22m∇2+V(r)+g∣ψ(r)∣2]ψ(r)i\hbar \frac{\partial \psi}{\partial t} = \left[-\frac{\hbar^2}{2m}\nabla^2 +V(r) + g|\psi(r)|^2\right]\psi(r)

右辺にg∣ψ∣2g|\psi|^2があることが本質です。左辺は時間微分なので、右辺が大きくなればなるほどψ\psiが強く増大するようになります。右辺にg∣ψ∣2g|\psi|^2の項があるおかげで、∣ψ∣|\psi|が大きいところから優先的にψ\psiが大きくなる”自己増幅”を表現しているのです。

そんなGP方程式は自己増殖の特徴だけでなく、渦の量子化という視点も持ち合わせます。

超流動の渦

超流動では渦と呼ばれる密度ゼロの領域がポツポツ発生します。その渦について、渦の強さ(循環)が整数倍の値しか取り得ないという際立った特徴があります。超流動状態ψ\psiの位相が揃いながら渦を作るという制約のために、位相を壊さない特定の量h/mh/mの整数倍に限定され、渦が一本一本数えられるという面白い性質が現れるのです。

超流動を回そう

そんな超流動状態ですが、ちょっと回すと簡単に渦ができます。回転の影響は古典力学でv′=v−Ω×rv'=v - \Omega \times rとかけます。運動量はp′=p−mΩ×rp' = p - m\Omega \times rとなるので、微分の項がその影響を受けて、

iℏ∂ψ∂t=[12m(−iℏ∇−mΩ×r)2+V(r)+g∣ψ(r)∣2]ψ(r)i\hbar \frac{\partial \psi}{\partial t} = \left[\frac{1}{2m}(-i\hbar \nabla - m \Omega \times r)^2 +V(r) + g|\psi(r)|^2\right]\psi(r)

と表記することができます。実は、先行研究によると、超流動体を回すと渦が生じ、高速回転すると三角格子が生まれるということが知られています。せっかくの方程式なので、これを数値計算して、格子構造が出現するかどうか試してみましょう！

数値計算

以下のコードを作成しました。Ω依存性と時間依存性の2種類になります。

Ω\Omega依存性

回転速度をちょっとづつ変えて行った時の変化をアニメーションにしました。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation

print("\n【2. Ω依存性アニメーションの準備を開始】")

# --- パラメータ設定 ---
hbar = 1.0
m = 1.0
g = 1.0
L = 10.0
N = 512 # 計算時間が長いため、Nを小さめに設定することを推奨
dx = L / N
x = np.linspace(-L/2, L/2, N)
X, Y = np.meshgrid(x, x)
R2 = X**2 + Y**2

# --- ダンピングと時間設定 ---
gamma = 0.02 # 少し強めのガンマで早く収束させる
dt = 0.002
total_steps_per_omega = 5000 # 各Ωでのステップ数

# --- Ωの範囲設定 ---
num_omegas = 20
omegas = np.linspace(0.0, 1.0, num_omegas)
final_states = []

# --- フーリエ空間の準備 ---
kx = 2 * np.pi * np.fft.fftfreq(N, d=dx)
ky = 2 * np.pi * np.fft.fftfreq(N, d=dx)
KX, KY = np.meshgrid(kx, ky)
K2 = KX**2 + KY**2

# ==========================================================
# === ステージ1: 各Ωでの最終状態を計算 ===
# ==========================================================
for i, Omega in enumerate(omegas):
    print(f"({i+1}/{num_omegas}) Ω = {Omega:.3f} の計算を開始...")

    # --- 時間発展演算子の設定 (Ωに依存するためループ内で毎回計算) ---
    propagator_complex_factor = -(gamma + 1j) / hbar
    K_kinetic_op = (hbar**2 * K2 / (2 * m))
    Ax = -Omega * Y
    Ay = Omega * X
    A_dot_k = Ax * KX + Ay * KY
    A2 = Ax**2 + Ay**2
    Gauge_op = (2 * A_dot_k + (m / hbar) * A2) * hbar / (2 * m)
    K_total_exponent = (K_kinetic_op + Gauge_op) * dt
    K_propagator = np.exp(propagator_complex_factor * K_total_exponent)
    V = 0.5 * R2
    V_propagator_half = np.exp(propagator_complex_factor * V * dt / 2)

    # --- 初期状態を毎回リセット ---
    np.random.seed(42)
    psi = np.exp(-R2) * (1 + 0.01 * (np.random.rand(N, N) - 0.5))
    psi = psi.astype(np.complex128)
    psi /= np.sqrt(np.sum(np.abs(psi)**2) * dx * dx)

    # --- 収束ループ ---
    for step in range(total_steps_per_omega):
        # スプリットステップ法
        g_propagator_half = np.exp(propagator_complex_factor * (g * np.abs(psi)**2) * dt / 2)
        psi *= V_propagator_half
        psi *= g_propagator_half
        psi_k = np.fft.fft2(psi)
        psi_k *= K_propagator
        psi = np.fft.ifft2(psi_k)
        g_propagator_half = np.exp(propagator_complex_factor * (g * np.abs(psi)**2) * dt / 2)
        psi *= g_propagator_half
        psi *= V_propagator_half
        psi /= np.sqrt(np.sum(np.abs(psi)**2) * dx * dx)
    
    # 最終状態の密度を保存
    final_density = np.abs(psi)**2
    final_states.append(final_density)
    print(f"-> Ω = {Omega:.3f} の計算完了。")

# ==========================================================
# === ステージ2: 保存した最終状態からアニメーションを作成 ===
# ==========================================================
print("\n全Ωの計算が完了。アニメーションを作成します...")
fig, ax = plt.subplots(figsize=(6, 6))
vmax = np.max(final_states) if final_states else 1.0
img = ax.imshow(final_states[0], extent=(-L/2, L/2, -L/2, L/2), cmap='inferno', vmin=0, vmax=vmax)
ax.set_xlabel("x")
ax.set_ylabel("y")
cb = fig.colorbar(img, ax=ax)
cb.set_label(r"Final State Density $|\psi|^2$")
title = ax.set_title("") # update関数で設定

def update_omega_dependent(i):
    img.set_array(final_states[i])
    title.set_text(f"Final State for $\Omega = {omegas[i]:.3f}$")
    return [img, title]

ani = animation.FuncAnimation(fig, update_omega_dependent, frames=len(omegas), blit=True)

# --- GIF保存 ---
output_filename_omega = 'animation_omega_dependent.gif'
print(f"アニメーションをGIFファイル ({output_filename_omega}) として保存しています...")
ani.save(output_filename_omega, writer='pillow', fps=3, dpi=120)
print(f"保存が完了しました: {output_filename_omega}")
plt.close(fig) # メモリを解放

結果、以下のようになりました。

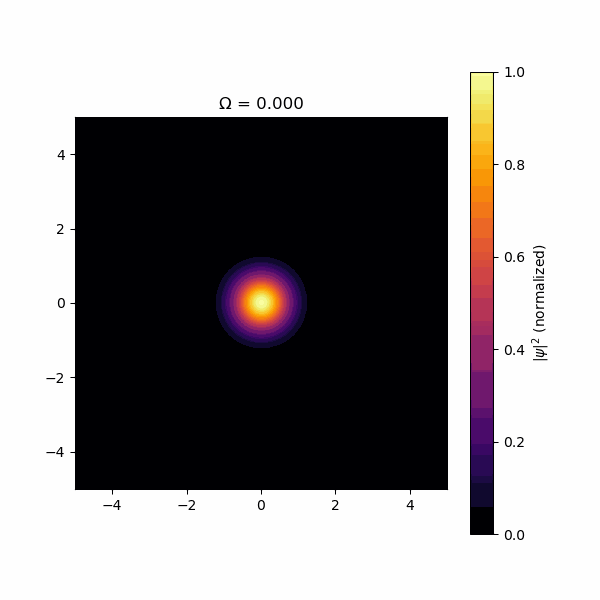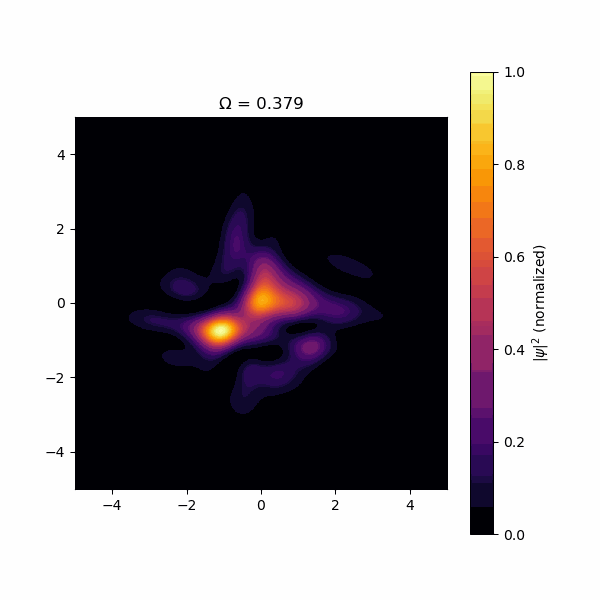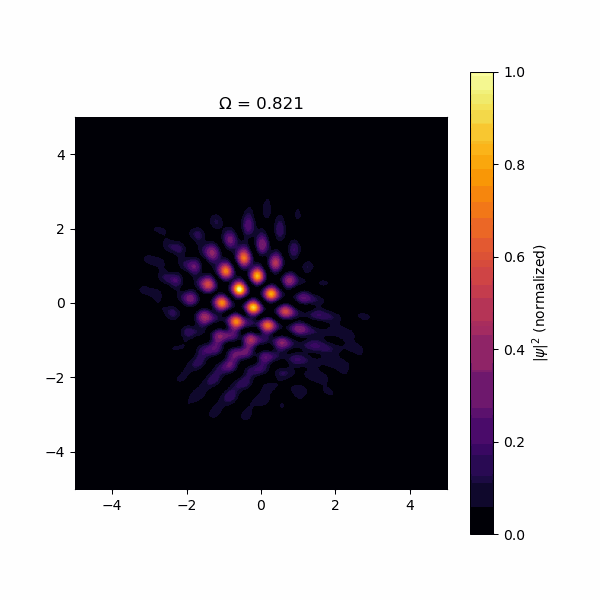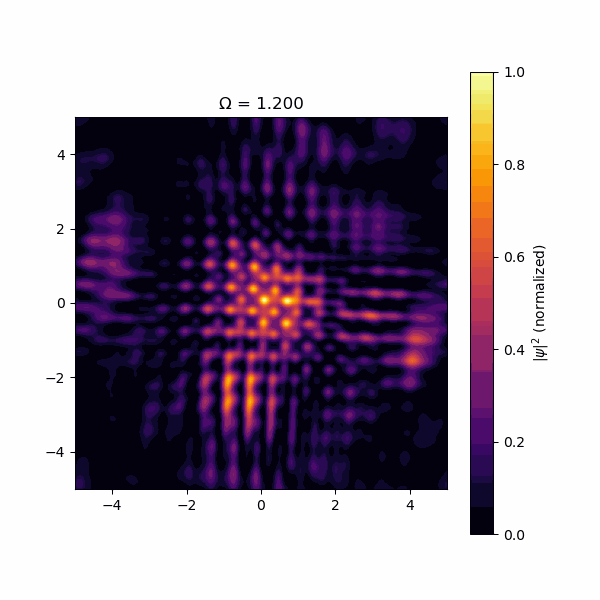
GPEパターン形成のΩ依存性

注意したいのは、渦は波動関数の振幅がゼロの場所なので、渦は暗い場所ということになります。このように、回転速度を上げて、Ω=0.8\Omega = 0.8程度になった時に格子構造が出現することが検証できました！遠心力で飛んで行かないように調和振動子ポテンシャルを入れてますが、Ω/ω>1\Omega/\omega>1になると束縛力が遠心力に負けるので、格子がばらけて飛んでいきます。残念ながら三角格子になりませんでしたが、それにはいくつか理由があります。

  1. 境界の形状

系のサイズが有限なので、その制約を受けます。加えて、系を製法上に離散化している関係で、渦が離散化の正方形状に止まりやすくなってしまっています。この現象をよくピン留めなんて言います。

  1. 三角格子と正方格子でエネルギーがそんなに変わらない

渦同士には斥力相互作用が生じるので三角格子を作りますが、そもそもエネルギー的にそこまで正方格子と変わらないので、先ほどのピン留めや境界の影響、有限サイズの効果の方がより強く効く結果かもしれません。

このようにして、超流動状態では離散化された渦が格子構造を生み出していることがわかりました。

時間依存性

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation

print("【1. 時間依存アニメーションの準備を開始】")

# --- パラメータ設定 ---
hbar = 1.0
m = 1.0
g = 1.0
L = 10.0
N = 1024 # 計算負荷に応じて 512 などに下げてください
dx = L / N
x = np.linspace(-L/2, L/2, N)
X, Y = np.meshgrid(x, x)
R2 = X**2 + Y**2

# --- ダンピングと時間設定 ---
gamma = 0.01  # ダンピングの強さ
dt = 0.001
total_steps = 20000 # ステップ数を20000に設定
num_frames = 100 # GIFのフレーム数
save_interval = total_steps // num_frames

# --- 固定パラメータ ---
Omega = 0.8

# --- アニメーション用リスト ---
frames_density = []
step_markers = []

# --- フーリエ空間と時間発展演算子の設定 ---
kx = 2 * np.pi * np.fft.fftfreq(N, d=dx)
ky = 2 * np.pi * np.fft.fftfreq(N, d=dx)
KX, KY = np.meshgrid(kx, ky)
K2 = KX**2 + KY**2

propagator_complex_factor = -(gamma + 1j) / hbar
K_kinetic_op = (hbar**2 * K2 / (2 * m))
Ax = -Omega * Y
Ay = Omega * X
A_dot_k = Ax * KX + Ay * KY
A2 = Ax**2 + Ay**2
Gauge_op = (2 * A_dot_k + (m / hbar) * A2) * hbar / (2 * m)
K_total_exponent = (K_kinetic_op + Gauge_op) * dt
K_propagator = np.exp(propagator_complex_factor * K_total_exponent)
V = 0.5 * R2
V_propagator_half = np.exp(propagator_complex_factor * V * dt / 2)

# --- 初期状態 ---
print("初期状態を準備しています...")
np.random.seed(42)
psi = np.exp(-R2) * (1 + 0.01 * (np.random.rand(N, N) - 0.5))
psi = psi.astype(np.complex128)
psi /= np.sqrt(np.sum(np.abs(psi)**2) * dx * dx)

# --- 時間発展ループ ---
print(f"Ω = {Omega:.2f}, γ = {gamma:.3f} で長時間の実時間発展を開始します...")
for step in range(total_steps):
    if step % save_interval == 0:
        print(f"  ステップ {step}/{total_steps} の状態を記録中...")
        density = np.abs(psi)**2
        frames_density.append(density)
        step_markers.append(step)

    # スプリットステップ法
    g_propagator_half = np.exp(propagator_complex_factor * (g * np.abs(psi)**2) * dt / 2)
    psi *= V_propagator_half
    psi *= g_propagator_half
    psi_k = np.fft.fft2(psi)
    psi_k *= K_propagator
    psi = np.fft.ifft2(psi_k)
    g_propagator_half = np.exp(propagator_complex_factor * (g * np.abs(psi)**2) * dt / 2)
    psi *= g_propagator_half
    psi *= V_propagator_half
    psi /= np.sqrt(np.sum(np.abs(psi)**2) * dx * dx)

# --- アニメーション作成 (振幅のみ) ---
print("アニメーションを作成しています...")
fig, ax = plt.subplots(figsize=(6, 6))
vmax = np.max(frames_density[-1]) if frames_density else 1.0
img = ax.imshow(frames_density[0], extent=(-L/2, L/2, -L/2, L/2), cmap='inferno', animated=True, vmin=0, vmax=vmax)
ax.set_xlabel("x")
ax.set_ylabel("y")
cb = fig.colorbar(img, ax=ax)
cb.set_label(r"$|\psi|^2$ (density)")
title = ax.set_title("") # update関数で設定

def update_time_dependent(i):
    img.set_array(frames_density[i])
    title.set_text(f"Time Evolution ($\Omega={Omega:.2f}$), Step={step_markers[i]}")
    return [img, title]

ani = animation.FuncAnimation(fig, update_time_dependent, frames=len(frames_density), blit=True)

# --- GIF保存 ---
output_filename_time = 'animation_time_dependent.gif'
print(f"アニメーションをGIFファイル ({output_filename_time}) として保存しています...")
ani.save(output_filename_time, writer='pillow', fps=10, dpi=120)
print(f"保存が完了しました: {output_filename_time}")
plt.close(fig) # メモリを解放

結果

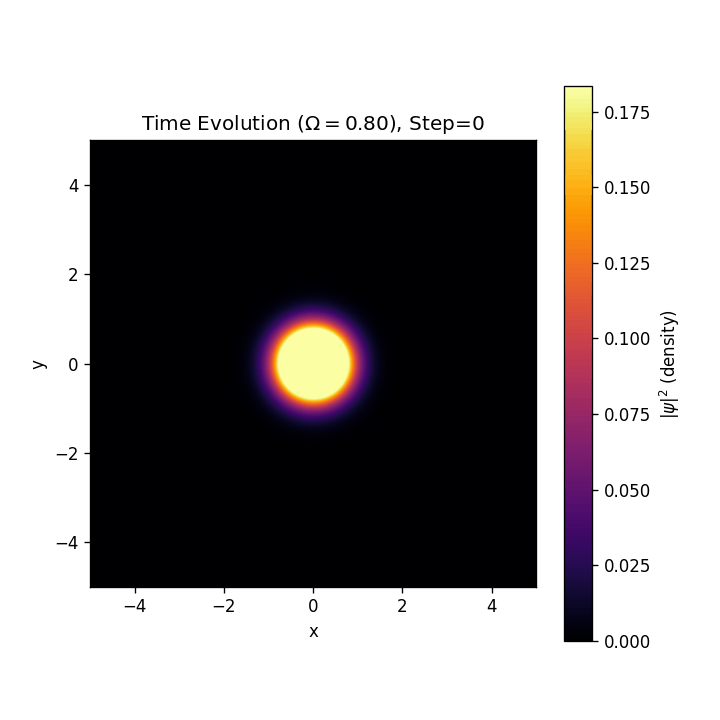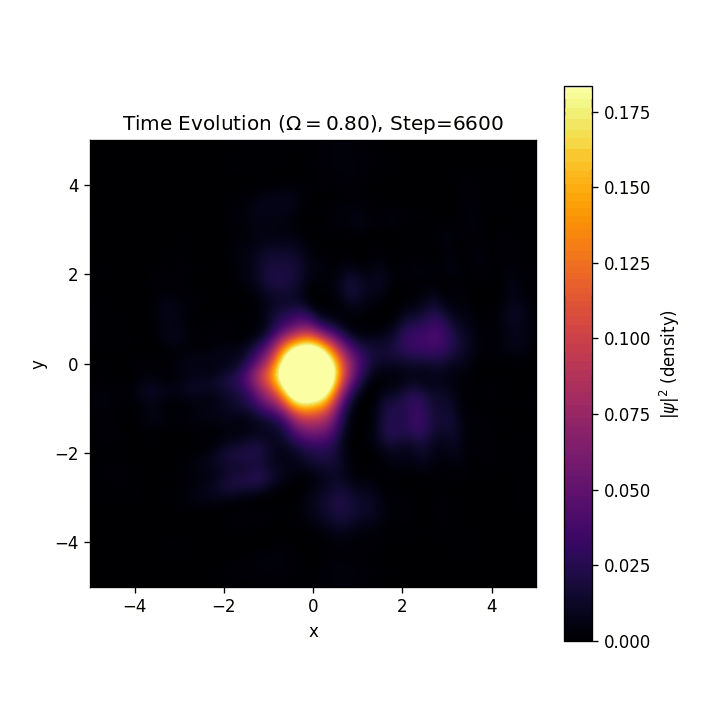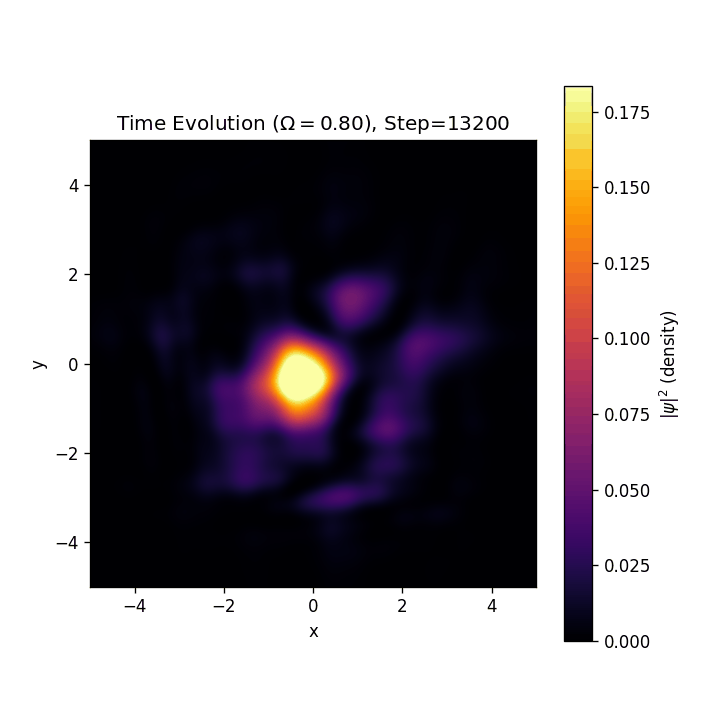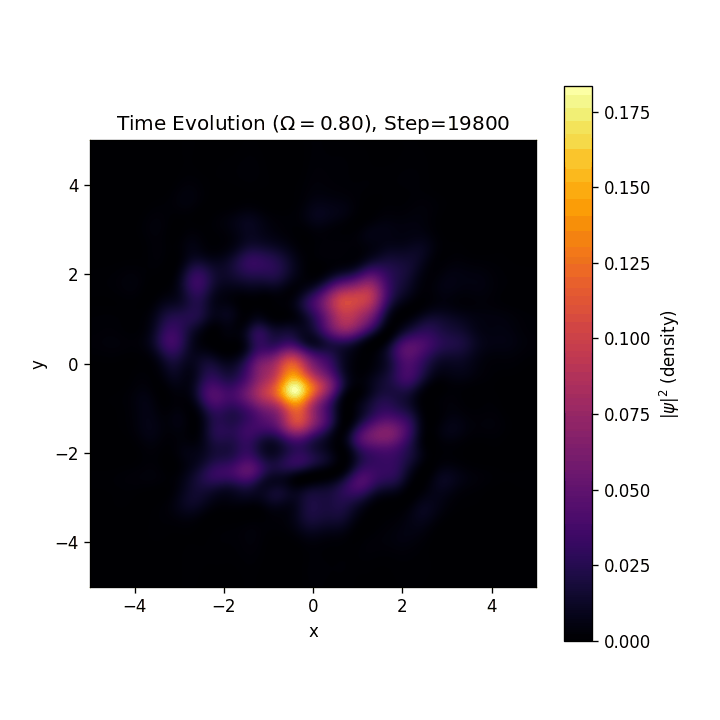
GPEパターン形成のΩ依存性

渦格子が生成したり壊れたりを繰り返しています。これに関してもいくつか仮説があり、それを発表しようかなというふうに思います。

  • 斥力相互作用により渦格子が壊れやすい

渦同士の斥力相互作用により、閉じ込めがないとすぐに拡散するのかもしれません。また、渦格子には格子振動のモードが生じています(トカチェンコモードと言います)。このモードと渦格子の斥力相互作用により、渦格子が壊れては生成し、生成してはトカチェンコモードで壊れを繰り返す、いわば時間的に準安定な構造を周期的に遷移している状態なのかもしれないというふうに考えました。この仮説が検証できれば面白いなというふうに感じます。

まとめ、感想

超流動体を回すと初めて渦格子が出現するというのが非常に興味深かったです。ある程度の速さで回して初めて格子ができるので、渦格子相転移のような現象が生じているのかなというふうにも感じました。相転移に加え、準安定状態の遷移描像が確立できれば嬉しいなと思いつつ、これからも計算していこうかなというふうに思います。

参考文献
Alexander L. Fetter “Rotating trapped Bose-Einstein condensates,“
Rev. Mod. Phys. 81, 647 (2009).

Gordon Baym,
“Vortex lattices in rapidly rotating Bose-Einstein condensates: Modes and correlation functions,“
Phys. Rev. A 69, 043618 (2004).

ガウス過程による回帰曲線の導出
量子計量テンソルとSLD計量、量子パラメータ推定について勉強中