ガウス過程による回帰曲線の導出

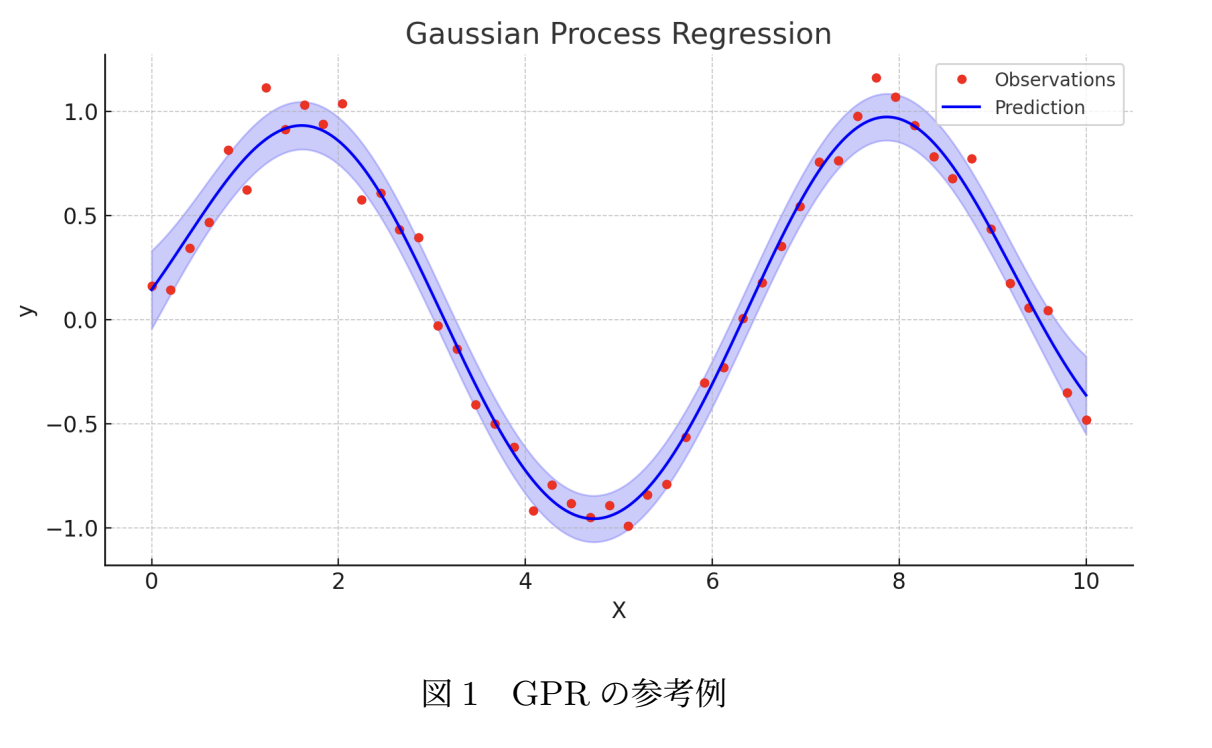
1 ガウス過程回帰

1.1 問題のモデル化

ガウス過程を用いて回帰曲線を求める方法を勉強したのでまとめます。

ハットなしの$z$は確率変数で、ハットありの$\hat{z}$は定ベクトルです。確率変数の時点ではその値がいくつか決まっていませんが、測定して値が確定すると、その値は定ベクトルになります。

この問題をもっと正確に定式化してみましょう。観測値が

$z=y+\epsilon, y=y(x), \epsilon\sim\mathcal{N}(0,\beta^{-1}I)$

のように表せることを仮定します。つまり、本質となる回帰曲線 $y=y(x)$ があって、そこからのずれはガウス分布に従うというモデルを考えているわけです。自然な誤差を表現するのにガウス分布は有用なのですね。

さて、与えられたデータセット $(x_{1},\hat{z}_{1}),\cdot\cdot\cdot,(x_{n},\hat{z}_{n})$ の情報から回帰曲線 $y = y(x)$ を導出したいわけですが、これだけしかない情報から元の回帰曲線を求めるのは非常に困難です。そこで、$y$もガウス分布に従ってしまうという非常に大胆な仮定をしてしまうんです。

この仮定が非常にクリティカルです。なぜなら、ガウス分布とガウス分布の和は、ガウス分布に従うという性質があるから、$z$もまたガウス分布に従うからです。さらにこの仮定に加えて、回帰曲線がデータセット $(x_{1},\hat{z}_{1}),\cdot\cdot\cdot,(x_{n},\hat{z}_{n})$ を通過するという条件のもと条件付き確率を計算します。すると、なんと不思議なことに回帰曲線に相当するものが魔法のように導出されてしまうのです。この点がガウス過程回帰のとんでもなく面白い点になります。

1.2 カーネル関数を用いて

ガウス過程による回帰をするにはカーネル関数 $k(x,y)$ が必要です。カーネル内積を扱った章と同様に、以下のようなベクトル空間(=再生核ヒルベルト空間)を考えてみましょう。

本当は代入写像が連続なヒルベルト空間のことを再生核ヒルベルト空間と定義するのですが、ムーア・アロンシャインの定理とリースの表現定理より、これらは同値になります。

証明は以下の通りです。

この関数で回帰曲線 $y(x)$ を

$y(x)=w\cdot\phi(x)$

のように表現します。モデル化 (3) の仮定より$y$ はガウス分布に従います。これを表現するために、$w\sim\mathcal{N}(0,I)$ を仮定します。この時、$y$もガウス分布 $\mathcal{N}(0,\Phi\Phi^{\top})$ に従います。

$w\sim\mathcal{N}(0,I) \implies y\sim\mathcal{N}(0,\Phi\Phi^{\top})$

ここで$\Phi$は以下のような行列です。

$\Phi\Phi^{\top}$の意味は明確です。

のように、各行列要素がカーネル関数になります。これをもって、$K\equiv\Phi\Phi^{\top}$ と書くのが自然でしょう。

$z=y+\epsilon$, $y\sim\mathcal{N}(0,K)$, $\epsilon \sim \mathcal{N}(0, \beta^{-1}I)$ であり、ガウス分布の和はまたガウス分布なので、この分布が

$z\sim\mathcal{N}(0,K+\beta^{-1}I)$

のように求まります。このように、なんの測定結果もなしの状況では、中心がゼロのガウス分布になります。

1.3 条件付き確率分布

今回の問題の再喝をしましょう。

新たな入力データ $x_{*}=x_{n+1},\cdot\cdot\cdot,x_{n+m}$ が追加されたとしましょう。この時 $z_{all}=z_{1},\cdot\cdot\cdot,z_{n+m}$ の確率分布は

$z_{all}\sim\mathcal{N}(0,K_{n+m}+\beta^{-1}I_{n+m})$

と表されます。ここで、

としています。入力データ $x=x_{1},\cdot\cdot\cdot,x_{n}$ に対する観測値がそれぞれ $\hat{z} = \hat{z}_{1},\cdot\cdot\cdot,\hat{z}_{n}$ と確定したとして、$z_{*}\equiv z_{n+1},\cdot\cdot\cdot,z_{n+m}$ の確率分布を求めることはできるでしょうか?

非常に面白いことに、多変量ガウス分布の一部の変数が定まった条件での条件付き確率分布は、またガウス分布になります。この分布は分散によって信頼区間を与えることができるので、「$z_{*}$ の値が○○~○○に入る確率が95%だよ」という形の推定をすることができます!

いざ、条件付き確率を求めましょう。条件なしの確率分布は

$z_{all}\sim\mathcal{N}(0,K_{n+m}+\beta^{-1}I_{n+m})$

$\Leftrightarrow p(z_{all})=\gamma \exp(-\frac{1}{2}\langle(K_{n+m}+\beta^{-1}I)^{-1}\begin{pmatrix}z\\ z_{*}\end{pmatrix},\begin{pmatrix}z\\ z_{*}\end{pmatrix}\rangle)$

となります。$\gamma$は正規化定数ですが、今回の議論では全く関係ないのでスルーします。以降の議論でも正規化定数は全く使用しません。測定により $z=\hat{z}$ が定まっている条件下での条件付き確率分布は

$p(z_{*}|\hat{z})=\gamma \exp(-\frac{1}{2}\langle(K_{n+m}+\beta^{-1}I)^{-1}\begin{pmatrix}\hat{z}\\ z_{*}\end{pmatrix},\begin{pmatrix}\hat{z}\\ z_{*}\end{pmatrix}\rangle)$

で与えられます。指数関数の中身を平方完成することを目論みます。

$K_{n+m}+\beta^{-1}I=\begin{pmatrix}K_{n}+\beta^{-1}I_{n}&k\\ k^{\top}&K_{m}+\beta^{-1}I_{m}\end{pmatrix}$

とブロックに分けます。ここで、

$K_{m}=\begin{pmatrix}k(x_{n+1},x_{n+1})&\dots&k(x_{n+1},x_{n+m})\\ \vdots&&\vdots\\ k(x_{n+m},x_{n+1})&\dots&k(x_{n+m},x_{n+m})\end{pmatrix}$

$k=k(x,x_{*})=\begin{pmatrix}k(x_{1},x_{n+1})&\dots&k(x_{1},x_{n+m})\\ \vdots&&\vdots\\ k(x_{n},x_{n+1})&\dots&k(x_{n},x_{n+m})\end{pmatrix}$

と簡略化した。また、

$(K_{n+m}+\beta^{-1}I)^{-1}=\begin{pmatrix}L_{11}&L_{12}\\ L_{21}&L_{22}\end{pmatrix}$

とします。元の行列が対称行列なので、$L_{12}^{\top}=L_{21}$。指数関数の中身は

$\langle\begin{pmatrix}L_{11}&L_{12}\\ L_{21}&L_{22}\end{pmatrix}\begin{pmatrix}\hat{z}\\ z_{*}\end{pmatrix},\begin{pmatrix}\hat{z}\\ z_{*}\end{pmatrix}\rangle=\langle L_{11}\hat{z},\hat{z}\rangle+2\langle L_{12}z_{*},\hat{z}\rangle+\langle L_{22}z_{*},z_{*}\rangle$

と表せます。 $z_{*}$ について平方完成するために、

$\langle L_{11}\hat{z},\hat{z}\rangle+2\langle L_{12}z_{*},\hat{z}\rangle+\langle L_{22}z_{*},z_{*}\rangle = \langle L_{11}\hat{z},\hat{z}\rangle+\langle L_{22}(z_{*}-a),(z_{*}-a)\rangle-\langle L_{22}a,a\rangle$

となるような$a$を求めます。$a$に課せられる条件は、

$\langle L_{12}z_{*},\hat{z}\rangle=-\langle L_{22}z_{*},a\rangle$

なので、これを満たすには

$a=-L_{22}^{-1}L_{12}^{\top}\hat{z}=-L_{22}^{-1}L_{21}\hat{z}$

とすれば良いことが簡単な計算でわかります。あとは行列 $L_{11},\cdot\cdot\cdot,L_{22}$ をそれぞれ計算して、$a$の表式に代入すると、

$a=k^{\top}(K_{n}+\beta^{-1}I_{n})^{-1}\hat{z}$

さらに、 $(K_{n}+\beta^{-1}I_{n})^{-1}\hat{z}=(c_{1},\cdot\cdot\cdot,c_{n})^{\top}$ とおけば、

というふうに簡略化して書くことができます。

$\langle(K_{n+m}+\beta^{-1}I)^{-1}\begin{pmatrix}\hat{z}\\ z_{*}\end{pmatrix},\begin{pmatrix}\hat{z}\\ z_{*}\end{pmatrix}\rangle=\langle L_{11}\hat{z},\hat{z}\rangle+\langle L_{22}(z_{*}-a),(z_{*}-a)\rangle-\langle L_{22}a,a\rangle$

となり、$z_{*}$ の関数として先ほどの条件付き確率を計算すると、

$p(z_{*}|\hat{z}) = \gamma' \exp(-\frac{1}{2}\langle L_{22}(z_{*}-a),(z_{*}-a)\rangle)$

が導かれます。まとめましょう。以下の式を再喝します。

$K_{n+m}+\beta^{-1}I=\begin{pmatrix}K_{n}+\beta^{-1}I_{n}&k\\ k^{\top}&K_{m}+\beta^{-1}I_{m}\end{pmatrix}$

$(K_{n+m}+\beta^{-1}I)^{-1}=\begin{pmatrix}L_{11}&L_{12}\\ L_{21}&L_{22}\end{pmatrix}$

上の式により、新規データ $x_{*}$ に対する平均と分散がそれぞれプロットできます。このように、$y=y(x)$ がガウス分布に従うという仮定のもとでは、データに対する条件付き確率分布がガウス分布になり、回帰曲線に対応するものがガウス過程の平均値の形で導出されることになります。