July 06, 2025

•

5 min read

太陽光にさらされる物質が、どうして温度一定になるのか？

#物理学 #理論 #古典物理 #天文

Table of Contents

🧩 はじめに

物質が太陽光に照らされ続けているのに、温度が発散せず一定に保たれるのはなぜか？
この素朴な問いに対する答えは、黒体放射と熱平衡の物理にあります。

このページでは、以下の流れでその仕組みを定量的に解説します：

黒体放射に関する3つの法則
放射平衡の数式と温度
球体モデルへの適用
黒体でも温度が発散しない理由
恒星の明るさとHR図への応用

📚 黒体放射の3つの法則

最も重要なのは プランクの法則 です。これは温度を持つすべての物質が放射をするという普遍法則を表しています。

プランクの法則から導かれるのが残り2つの法則だと理解すると見通しが良くなります。

1. プランクの法則（放射スペクトル）

黒体が温度 $T$ で放射する波長 $\lambda$ におけるスペクトル輝度（単位立体角あたりのエネルギー密度）：

B_\lambda(\lambda, T) = \frac{2hc^2}{\lambda^5} \cdot \frac{1}{e^{\frac{hc}{\lambda kT}} - 1}

$h$ : プランク定数、 $c$ : 光速、 $k$ : ボルツマン定数
単位: $\mathrm{W\,m^{-2}\,sr^{-1}\,m^{-1}}$

この式が黒体放射の全ての情報を持っており、山なりの関数形になる。

2. ウィーンの変位則（ピーク波長）

\lambda_{\text{max}} = \frac{b}{T}, \quad b \approx 2.898 \times 10^{-3}\,\mathrm{m \cdot K}

高温になるほど $\lambda_{\text{max}}$ は短波長側（青）へシフト。

プランクの法則のピークがこの法則を満たす。

3. ステファン＝ボルツマンの法則（総放射パワー）

P = \epsilon \cdot \sigma \cdot A \cdot T^4

$\epsilon$ : 放射率（黒体なら $\epsilon = 1$ ）
$\sigma = 5.670 \times 10^{-8}\,\mathrm{W/m^2 \cdot K^4}$
$A$ : 表面積、 $T$ : 絶対温度

放射エネルギーは温度の4乗に比例して急増する(重要)。

🔁 吸収と放射のエネルギーバランス

ここが最も重要です。 実は地球(黒体)も温度さえ持っていれば、エネルギーを放射します。 その放射強度はプランク分布の積分で計算することができ、それがステファンボルツマンの法則になります。あまねく全ての物質が黒体放射するというところが、地球の過剰な温度上昇を防いでいるのですね。

このように、太陽から受けるエネルギーと、地球が放射するエネルギーが釣り合うことで、地球の温度は一定に保たれ続けます。その 熱平衡 を定式化すると、以下のように表現できます。

物体が太陽光に照らされたときの熱平衡条件：

\text{吸収エネルギー} = \text{放射エネルギー}

吸収エネルギー（太陽から）：

P_{\text{in}} = \alpha S A

$S$ : 太陽定数（ $1361\,\mathrm{W/m^2}$ ）
$\alpha$ : 吸収率（黒体で $\alpha = 1$ ）

放射エネルギー（物体から）：

P_{\text{out}} = \epsilon \sigma A T^4

熱平衡条件：

これら二つが釣り合うので、

\alpha S = \epsilon \sigma T^4 \quad \Rightarrow \quad T = \left( \frac{\alpha S}{\epsilon \sigma} \right)^{1/4}

🌍 球体モデル：地球や恒星への応用

球体の吸収面積と放射面積は異なるため、エネルギー収支は次のように変形されます：

吸収エネルギー：

P_{\text{in}} = \alpha S \cdot \pi R^2

放射エネルギー：

P_{\text{out}} = \epsilon \sigma \cdot 4\pi R^2 \cdot T^4

熱平衡条件：

\alpha S \cdot \pi R^2 = \epsilon \sigma \cdot 4\pi R^2 \cdot T^4 \quad \Rightarrow \quad T = \left( \frac{\alpha S}{4 \epsilon \sigma} \right)^{1/4}

📊 地球の放射平衡温度（例）

$\alpha = 0.7$
$\epsilon = 1$
$S = 1361\,\mathrm{W/m^2}$

T = \left( \frac{0.7 \times 1361}{4 \times 5.670 \times 10^{-8}} \right)^{1/4} \approx 254\,\mathrm{K}

温室効果を含まない地球の理想的放射温度がこれです。 254Kは-19℃なので流石に低すぎますが、これは大気などの温室効果を考慮に入れてない点や、氷床のような真っ白の地表が太陽光を反射する効果などを考慮に入れていない点を反映しています。

🔥 黒体でも温度が発散しない理由

黒体（ $\alpha = \epsilon = 1$ ）のような最大限光を吸収する物質であっても、温度が上がると放射エネルギーは $T^4$ に比例して急増します。

P_{\text{out}} = \sigma T^4

これにより、どれだけ吸収しても、放射の自己制御効果により温度が自然に平衡点へ落ち着きます。

✨ 恒星の明るさと温度の関係（HR図）

恒星の放射出力（光度） $L$ はステファン＝ボルツマンの法則から：

L = 4\pi R^2 \cdot \sigma T^4

$R$ : 恒星の半径
$T$ : 表面温度

この関係を使うと、光度と温度を軸にした Hertzsprung–Russell図（HR図） が描けます。簡単に言えば、星の表面温度(横軸)と明るさ(縦軸)を両対数プロットした図です。この図から恒星の性質を分類することができます。

HR図

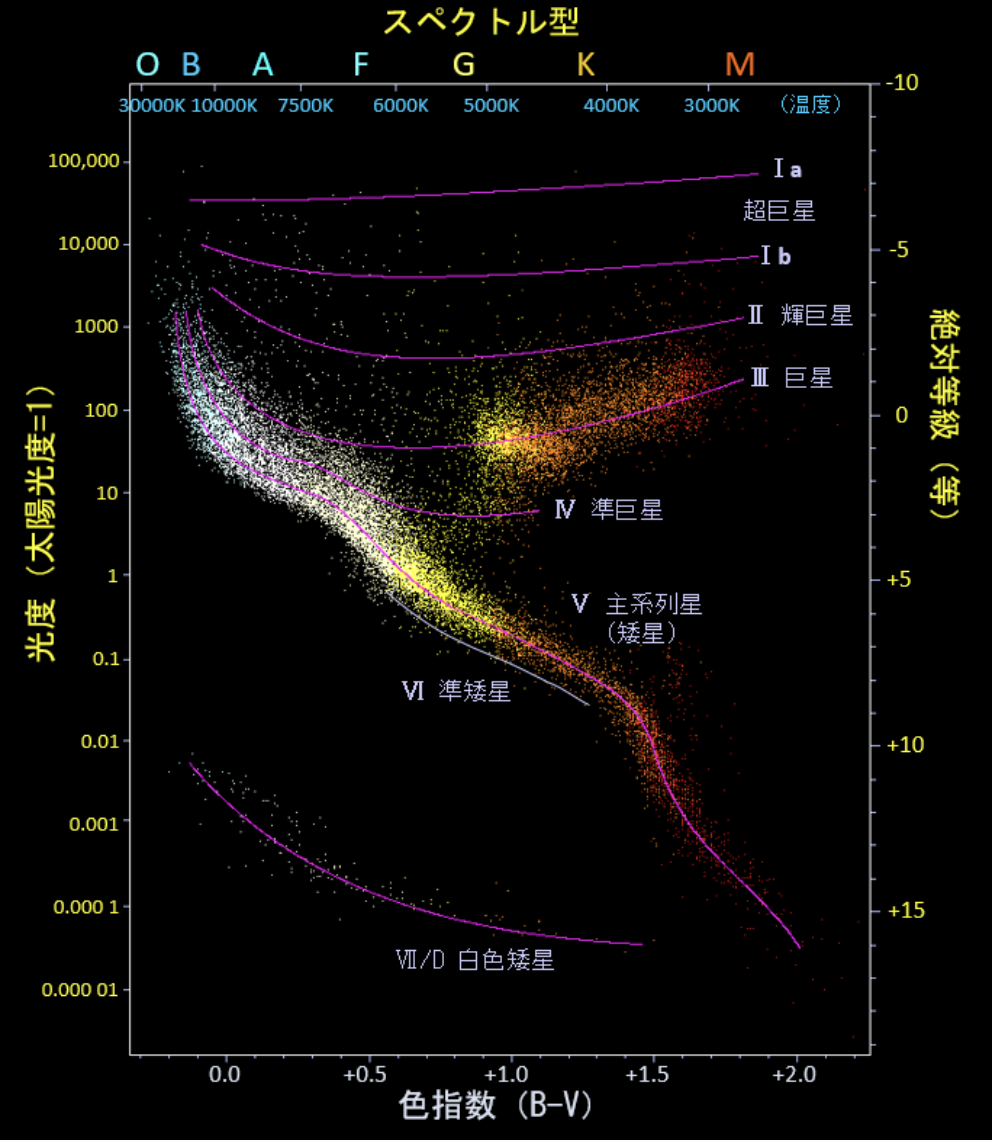
画像出典：天文学辞典 - Hertzsprung-Russell (HR) 図

HR図の特徴：

横軸：温度（右に行くほど低温、対数軸）
縦軸：光度（対数軸）

主系列（Main Sequence）

恒星の大部分は、核融合で安定したエネルギーを供給しており、 $L \propto T^4$ に近い関係に従う。

例：太陽と比較

恒星	温度 $T$	半径 $R$	光度 $L$
太陽	$5778\,\mathrm{K}$	$1\,R_\odot$	$1\,L_\odot$
シリウスA	$9900\,\mathrm{K}$	$1.7\,R_\odot$	$25\,L_\odot$ （観測値）

恒星の色（温度）と明るさ（光度）を結ぶ物理的裏付けが、黒体放射にある。

📊 HR図における進化経路の特徴

フェーズ	温度 $T$	半径 $R$	光度 $L$	HR図での動き
主系列	中～高	中	$L \sim M^{3.5}$	左上～右下の帯状
赤色巨星	低	非常に大	高（ $T$ 低いが $R$ ↑）	右上へ移動
白色矮星	非常に高	小さい	小さい	左下
高質量星の終焉	---	崩壊	---	HR図外（中性子星/BH）

🔭 実例：恒星の位置比較（HR図）

恒星	温度 ( $\mathrm{K}$ )	半径 ( $R_\odot$ )	光度 ( $L_\odot$ )	進化段階
太陽	$5778$	$1$	$1$	主系列
ベテルギウス	$3500$	$887$	$100,000$	赤色超巨星
シリウスB	$25,000$	$0.008$	$0.03$	白色矮星

✅ まとめ

恒星の放射特性は黒体放射に支配される（ $L = 4\pi R^2 \sigma T^4$ ）
HR図は恒星の進化を光度 vs. 温度の関係で描いた地図
各進化段階で、温度・半径・光度がどう変わるかを理解することで、HR図の読み解きが可能

📚 関連用語（補足）

主系列星：水素燃焼による安定した状態の恒星
巨星/超巨星：核融合の次段階（He燃焼以降）で膨張
白色矮星：燃料を失った後の高密度残骸
中性子星／ブラックホール：高質量星の死後の極限状態

🌌 恒星の温度・半径・質量・光度を見れば、その進化段階・寿命・最終運命まで読み解くことができます。

✅ まとめ

黒体は温度に応じて $T^4$ に比例した放射を行う。
吸収と放射が釣り合うことで、温度は自然に一定になる。
球体では放射面積が増えるため、平面モデルより温度が低くなる。
HR図における恒星の位置は、ステファン＝ボルツマン法則と核融合の持続によって決まる。

📜 おまけ：黒体放射とプランク分布の歴史的背景と理論

19世紀末、物理学者たちは「加熱した物体が放射する光のスペクトル」を精密に測定し始めました。その中で、黒体放射の理論的説明が物理学最大の難題の一つとして現れました。

🔥 黒体とは？

黒体とは、あらゆる波長の電磁波を完全に吸収し、同じ温度での放射を最大限に行う理想的な物体です。
実際には、炭素粒子や黒塗りの空洞などが黒体の近似として使われます。

🧨 紫外破綻

当時の古典物理学（レイリー・ジーンズの法則）は、黒体の放射エネルギーが波長の短い（高周波）側で無限大に発散するという破綻をもたらしました：

B_\lambda^{\text{RJ}}(\lambda, T) \propto \frac{1}{\lambda^4}

この予言は観測と著しく矛盾しており、「紫外線破綻（Ultraviolet Catastrophe）」と呼ばれました。

🌌 プランクの登場と量子論の夜明け（1900年）

マックス・プランク（Max Planck） は、放射のエネルギーが連続的ではなく 量子化されている（離散的） と仮定し、黒体放射の正しい式を導きました。エネルギーをまるで離散的な粒子のように捉えたのですね。

✅ プランク分布の式

B_\lambda(\lambda, T) = \frac{2hc^2}{\lambda^5} \cdot \frac{1}{e^{\frac{hc}{\lambda kT}} - 1}

$h$ : プランク定数
$c$ : 光速
$k$ : ボルツマン定数

この式は 観測と完全に一致 し、量子論の基礎を築く決定的な成果となりました。

✴ プランク分布からステファン＝ボルツマンの法則を導く

総放射エネルギー（単位面積あたり）：

P = \int_0^\infty \pi B_\lambda(\lambda, T) \, d\lambda

※ $\pi$ は立体角積分による半球方向への放射の統合

変数変換：

波長 $\lambda$ を無次元変数 $x$ に変換：

x = \frac{hc}{\lambda kT} \quad \Rightarrow \quad \lambda = \frac{hc}{kTx}, \quad d\lambda = -\frac{hc}{kT x^2} dx

積分を整理：

P = \pi \int_0^\infty \frac{2hc^2}{\lambda^5} \cdot \frac{1}{e^{hc/\lambda kT} - 1} \, d\lambda

変換後：

P = \frac{2\pi k^4 T^4}{h^3 c^2} \int_0^\infty \frac{x^3}{e^x - 1} dx

積分値：

\int_0^\infty \frac{x^3}{e^x - 1} dx = \frac{\pi^4}{15}

結果：ステファン＝ボルツマン定数の導出

P = \sigma T^4, \quad \text{where} \quad \sigma = \frac{2\pi^5 k^4}{15 h^3 c^2}

この導出により、ステファン＝ボルツマンの法則は量子論的基礎を持つ理論として再構築されました。

歴史的意義まとめ

年	出来事
1879	ステファンが経験的に $T^4$ 法則を発見
1884	ボルツマンが理論的に $T^4$ 法則を導出（統計力学）
1900	プランクが量子仮説を導入し、分布関数を導出
20世紀以降	量子力学、場の量子論、熱輻射の理論的礎に

黒体放射の理解は、量子力学の誕生そのものと直結しています。

✨ まとめ

黒体放射の観測から量子論の基礎が築かれた
プランク分布はすべての熱放射の「基本分布」
ステファン＝ボルツマンの法則はその積分結果である
天体・気候・放射冷却など、あらゆる分野に応用されている

🌌 1つの放射スペクトルから始まった議論が、現代物理の礎になりました。

ド・ラームコホモロジー入門

分数量子ホール効果に潜む数論とトポロジカル秩序の圏論的記述