リーマンの明示公式で素数階段を再現してみた！

素数階段の謎とリーマンの公式

素数（2, 3, 5, 7, …）って、どういうルールで現れるんでしょうか？この問題は、昔から多くの数学者を悩ませてきた超難問です。素数の並びをグラフにしてみると、素数計数関数 $\pi(x)$、通称 「素数階段」 と呼ばれるギザギザのグラフが描けます。

見ての通り、かなり不規則ですよね。こんなバラバラなものを、一本の綺麗な数式で書くことなんてできるんでしょうか？

まさかの、この階段関数を明示できる公式が存在します！ それが以下のリーマンの明示公式です。

リーマンの明示公式とは

19世紀の天才数学者リーマンは「できる！」と言いました。そして、素数の分布がリーマンゼータ関数 $\zeta(s)$ の零点（ゼロてん）という、ある特別な数字たちによって完璧に記述できることを示す、とんでもない公式を導き出しました。それがリーマンの明示公式です。

要するに、ゼータ関数の零点という「基本周波数」を全部足し合わせると、素数階段のギザギザの「メロディー」が再現できる、という驚くべき内容です。本当にそんなことが可能なのか、理論を追いながら、最後は実際にPythonで計算して検証してみましょう！

解析の下準備：扱いやすい関数への置き換え

素数階段 $\pi(x)$ は扱いにくい？

いきなり素数階段 $\pi(x)$ を料理しようとしても、素数のところでいきなり「カクン」と不連続に折れ曲がるので、微分などの数学的な道具が使いにくく、非常に扱いにくいのです。そこで、数学者たちはもっと解析と相性の良い「相棒」を考え出しました。それがフォン・マンゴルト関数です！

フォン・マンゴルト関数 $\psi(x)$

そこで登場するのが、上記のフォン・マンゴルト関数 $\Lambda(n)$ を使って定義されるチェビシェフ関数 $\psi(x)$ です。

これは、素数 $p$ だけでなく、$p^2, p^3$ といった「素数の仲間たち」の場所でもジャンプする、いわば「重み付き」の素数階段です。なぜこんな一見複雑なものを持ち出すかというと、この $\psi(x)$ こそが、ゼータ関数と非常に美しい関係で結ばれているからです。

この綺麗な関係式のおかげで、複素解析の強力なツールを使って、素数の世界の深層にダイブすることができるようになるのです。

いざ、明示公式の導出へ！

ここからが本番です。$\psi(x)$ とゼータ関数を結びつける複素積分（ペロンの公式）を評価することで、$\psi(x)$ の正体を暴いていきます。

この積分の計算は「留数定理」という必殺技を使います。ものすごく雑に言うと、「積分の値は、中身が無限大になる点（極）の情報だけで決まる」というものです。調べてみると、この積分の中身には4種類の「極」があることがわかります。

1. $s=1$ の極: ここから、素数分布の滑らかな平均線を示す主要項 $x$ が出てきます。これが全体の骨格です。

2. $s=\rho$ の極 (非自明な零点): ここから、階段のギザギザを再現する振動項 $-\sum_{\rho} \frac{x^\rho}{\rho}$ が出てきます。各零点 $\rho$ がそれぞれ一つの「波」に対応し、それらを全て足し合わせることで、あの不規則な揺らぎが生まれるのです。これが素数の音楽の正体です！

3. $s=-2k$ の極 (自明な零点): 負の偶数にある零点たちです。これらは、グラフの高さを微調整する補正項 $-\frac{1}{2}\log(1 - x^{-2})$ を与えます。

4. $s=0$ の極: 最後に、全体のオフセットを調整する定数項 $-\log(2\pi)$ が出てきます。

これら4つのパーツを全部ガチャンコすると、$\psi(x)$ の完璧な設計図、明示公式が完成します。

最終調整：素数そのものを抜き出す

さて、$\psi(x)$ の完璧なレシピは手に入りましたが、これにはまだ素数以外の情報（$p^2, p^3$ など）が混ざっています。これらを取り除いて、純粋な素数だけの階段 $\pi(x)$ に戻すための「フィルター処理」が必要です。これも数式で書けます。

まず、積分を使って中間関数 $\Pi(x)$ へと変換し（ステップ1）、

次に、メビウスの反転公式というフィルターをかけて、不要な素数冪の成分を取り除きます（ステップ2）。

これでようやく、ゼータ関数の零点から、素数階段そのものを再現する準備が整いました！

実際に計算してみた！

理論はこれくらいにして、実際にこの数式をPythonコードに落とし込んで、素数階段が再現できるか試してみましょう。コードは、これまで会話で作り上げてきた最終版（高精度版）です。

import numpy as np
import matplotlib.pyplot as plt
from sympy import primepi, mobius
from scipy.integrate import quad
from matplotlib.animation import FuncAnimation

# リーマンゼータ関数の非自明ゼロ点（虚数部γ）のリスト
ZETA_ZEROS_IMAG = [
    14.1347251417, 21.0220396388, 25.0108575801, 30.4248761259,
    32.9350615877, 37.5861781588, 40.9187190121, 43.3270732809,
    48.0051508811, 49.7738324777, 52.9703214777, 56.4462476970,
    59.3470440030, 60.8317785253, 65.0858034723, 67.0798105295,
    69.5464017112, 72.0671576745, 75.7046906990, 77.1448400688,
    79.3373750202, 82.9103808541, 84.7354929805, 87.4252746132,
    88.8091112275, 92.4918992706, 94.6513440411, 95.8706342283,
    98.8311942181, 101.3178510060, 103.7255380400, 105.446623052,
    107.141466323, 111.029535543, 111.874659177, 114.320220915,
    116.226680321, 118.790782866, 121.370125002, 122.946829244,
]

def von_mangoldt_psi_approx(x, num_zeros):
    if x <= 1: return 0
    x_c = np.complex128(x)
    approximation = x_c - np.log(2 * np.pi) - 0.5 * np.log(1 - x_c**(-2))
    for i in range(num_zeros):
        gamma = ZETA_ZEROS_IMAG[i]
        rho = 0.5 + 1j * gamma
        approximation -= (x_c**rho / rho) + (x_c**np.conj(rho) / np.conj(rho))
    return np.real(approximation)

def integrand_for_Pi(t, num_zeros):
    if t <= 1: return 0
    psi_t = von_mangoldt_psi_approx(t, num_zeros)
    return psi_t / (t * np.log(t)**2)

def riemann_prime_power_pi_approx(x, num_zeros):
    if x < 2: return 0
    psi_x = von_mangoldt_psi_approx(x, num_zeros)
    term1 = psi_x / np.log(x)
    integral_term, _ = quad(integrand_for_Pi, 2, x, args=(num_zeros,))
    return term1 + integral_term

def final_prime_pi_approx(x_vals, num_zeros):
    pi_approx_vals = []
    for x in x_vals:
        s = 0
        n_max = int(np.floor(np.log(x) / np.log(2))) if x > 1 else 1
        for n in range(1, n_max + 1):
            mu_n = mobius(n)
            if mu_n == 0: continue
            Pi_val = riemann_prime_power_pi_approx(x**(1/n), num_zeros)
            s += (mu_n / n) * Pi_val
        pi_approx_vals.append(s)
    return np.array(pi_approx_vals)

# --- 描画 ---
x_max = 50
num_zeros_to_use = 40
num_points = 500
x_vals = np.linspace(2, x_max, num_points)
actual_pi = np.asarray(np.vectorize(primepi)(np.floor(x_vals)), dtype=int)
formula_pi = final_prime_pi_approx(x_vals, num_zeros_to_use)

plt.style.use('dark_background')
fig, ax = plt.subplots(figsize=(14, 9))
ax.step(x_vals, actual_pi, where='post', label='Actual Number of Primes (primepi)', color='#66B2FF', linewidth=2.5)
ax.plot(x_vals, formula_pi, label=f'Riemann Formula Approx. ({num_zeros_to_use} zeros)', color='#FF7F7F', linewidth=1.8)
ax.set_title("Prime-Counting Function vs. High-Accuracy Riemann Formula", fontsize=18, pad=20)
ax.set_xlabel('x', fontsize=14)
ax.set_ylabel('π(x) - Number of primes below x', fontsize=14)
ax.grid(True, linestyle='--', alpha=0.25)
ax.set_xlim(0, x_max)
ax.set_ylim(bottom=0, top=max(actual_pi) + 2)
ax.legend()
plt.show()

数値計算の結果

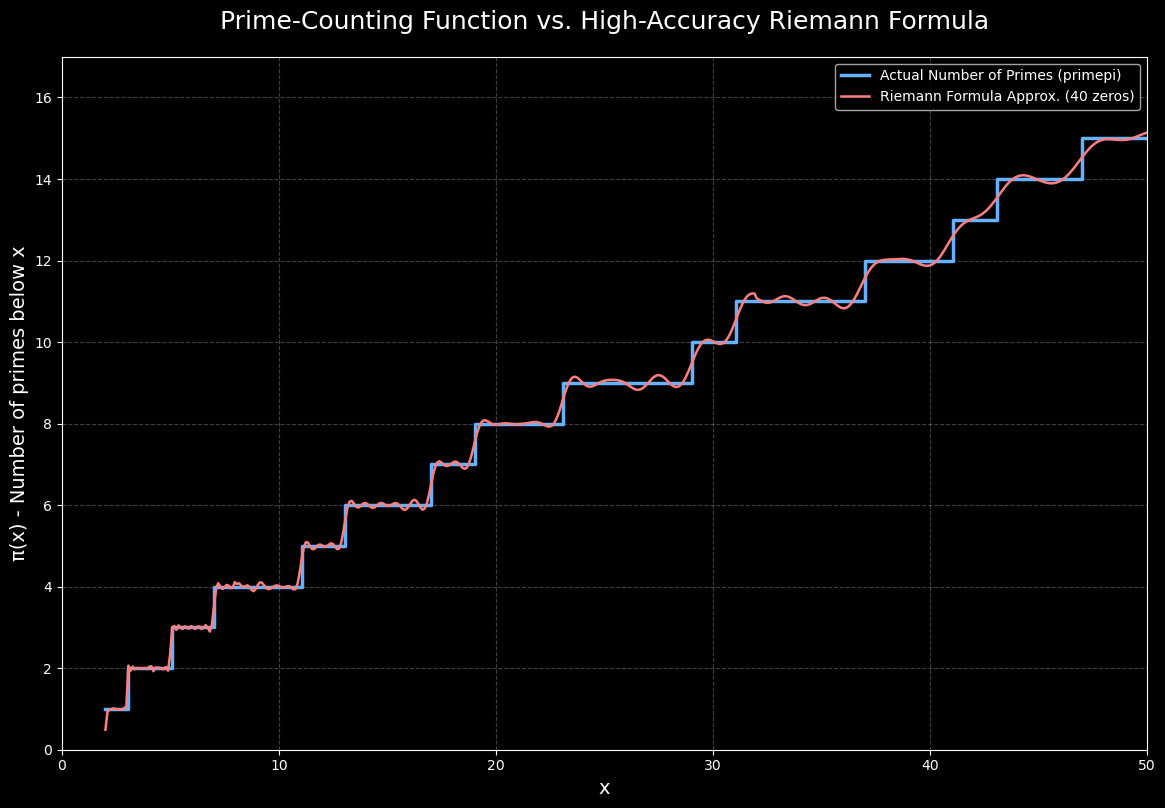
感動的ですね…！！

上のグラフが、実際にPythonで計算した結果です。青い線が実際の素数の個数をプロットした「素数階段」、そして赤い線が、ゼータ関数の零点を40個だけ使ってリーマンの明示公式から計算した近似曲線です。

驚くべきことに、滑らかな連続関数であるはずの明示公式が、素数という離散的な存在の出現を見事に捉え、ギザギザの階段のど真ん中を正確に貫いているのがわかります。

まとめと考察

素数階段 $\pi(x)$ を記述するリーマンの明示公式への道のりは、以下のようにまとめられます。

1. 解析が困難な $\pi(x)$ を、ゼータ関数と直結するチェビシェフ関数 $\psi(x)$ に置き換える。
2. ペロンの公式と留数定理という複素解析の道具を用いて、$\psi(x)$ をゼータ関数の零点と極の情報を含む代数的な式（明示公式）で表現する。
3. 得られた $\psi(x)$ の明示公式を、積分とメビウス反転を用いて $\pi(x)$ の表現に逆変換する。

この事実は、素数の分布という離散的で不規則に見える数論の問題が、ゼータ関数の零点の配置という複素平面上の連続的で解析的な構造によって、完全に支配されていることを示唆しています。特に、零点の実部がすべて $1/2$ であるというリーマン予想がもし真実であれば、素数の分布の誤差が可能な限り小さくなることも知られており、この二つの世界の繋がりは現代数学における最も重要で深遠なテーマの一つであり続けています。

参考文献

実はリーマンの原論文はたったの8ページで、現代では英語訳されて読みやすくなっています。これを機に読んでみると面白いかもしれません。

• Riemann, B. “Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse.” Monatsberichte der Berliner Akademie, (1859).
• Edwards, H. M. Riemann’s Zeta Function. Dover Publications, 2001.
• Titchmarsh, E. C. The Theory of the Riemann Zeta-Function. Oxford University Press, 1986.